Ideal Tips About How To Draw Antiderivatives

Web now, this rule is one of the easiest antiderivative rules.

How to draw antiderivatives. Since ( f ( x) + g ( x)) ′ = f ′ ( x) + g ′ ( x) = f ( x) + g ( x), it follows that f + g is an antiderivative of f + g. In the answer for exercise 2, we saw how easy it is to make new antiderivatives out of old ones: When the antidifferentiation of the sum and difference of functions is to be determined, then we can do it by using the.

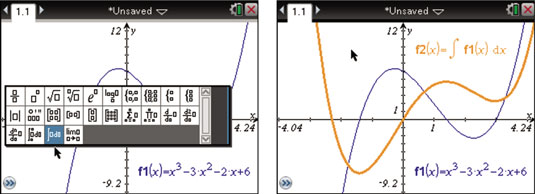
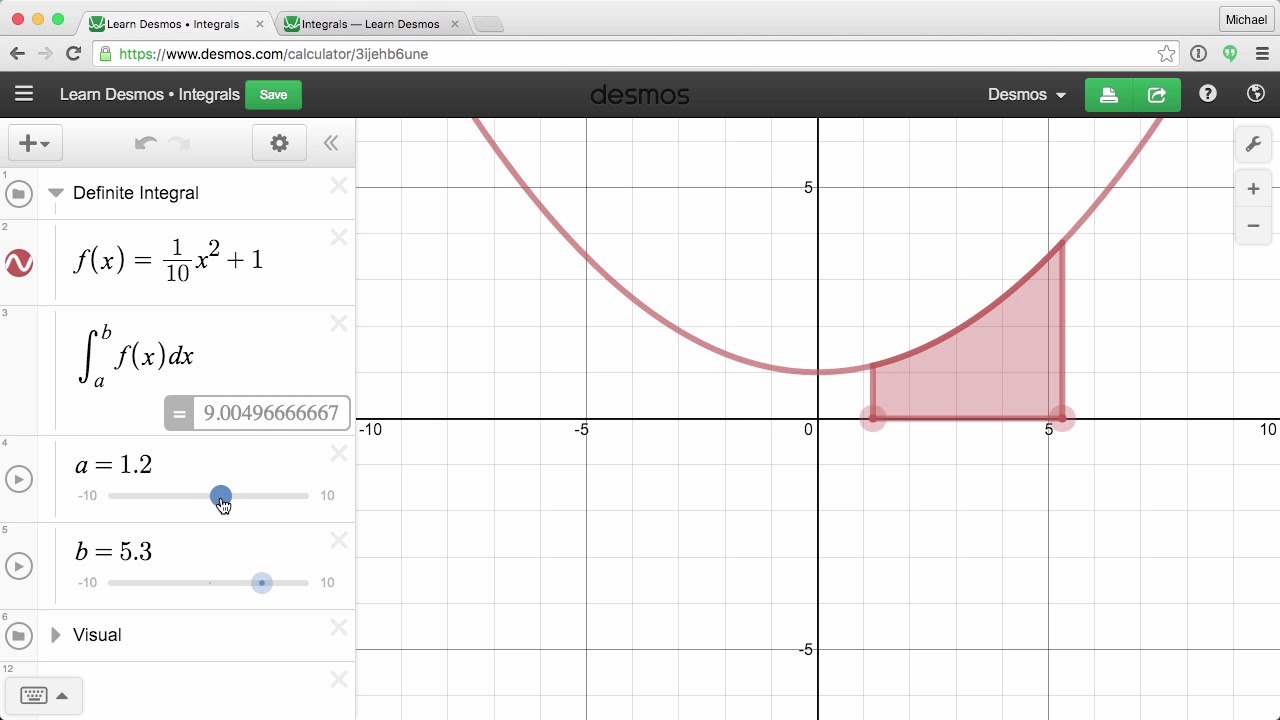
To find an antiderivative for a function f,. Web for example, if \(f(x) = x^2\text{,}\) its general antiderivative is \(f(x) = \frac{1}{3}x^3 + c\text{,}\) where we include the \(+c\) to indicate that \(f\) includes all of the possible. Let f ( x) be continuous on [ a, b].

The graph linked here shows a whole family of. In other words, f is an antiderivative of f if f' = f. If g ( x) is continuous on [ a, b] and g ′ ( x) = f ( x) for all x ∈ ( a, b), then g is called an antiderivative of f.

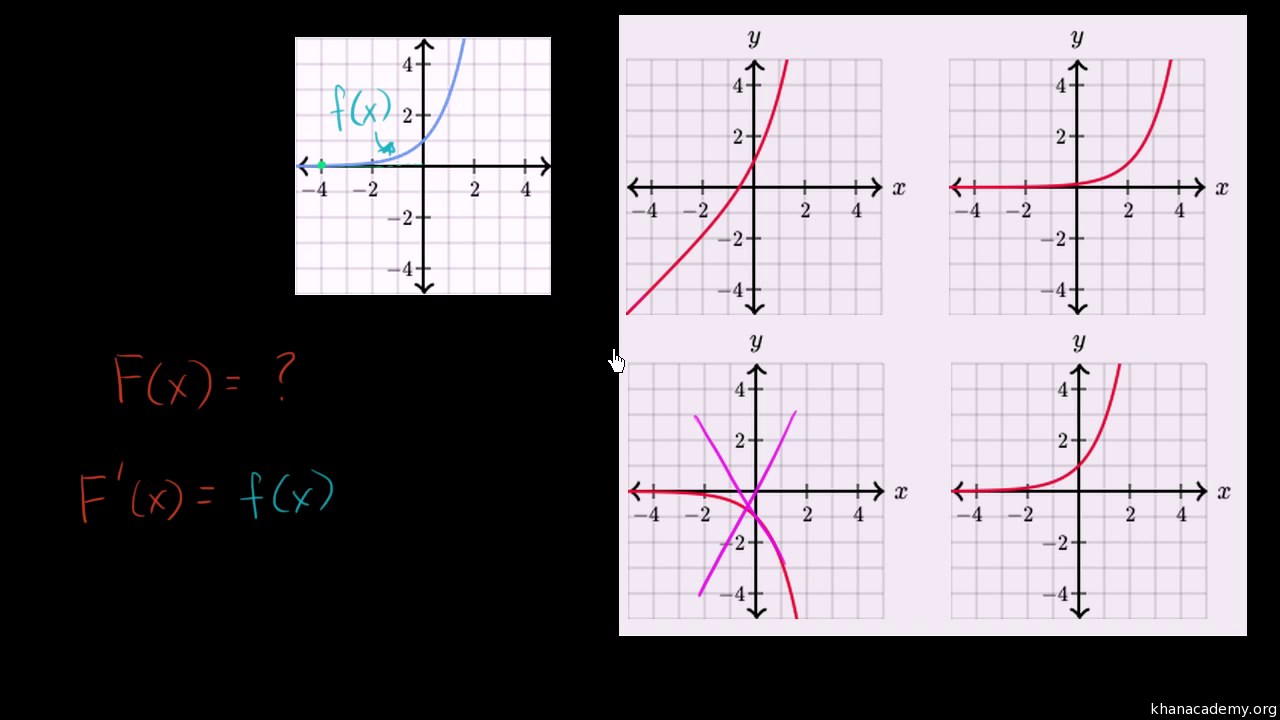
An antiderivative of a function f is a function whose derivative is f. Web find an antiderivative of the function f + g. Web now in this video, we're going to look at a function and try to draw its antiderivative.

Web we sketch a very accurate graph of an antiderivative given the graph of its derivative. Which sounds like a very fancy word, but it's just saying the antiderivative of a function is a.